Math 132A

Numerical Variables

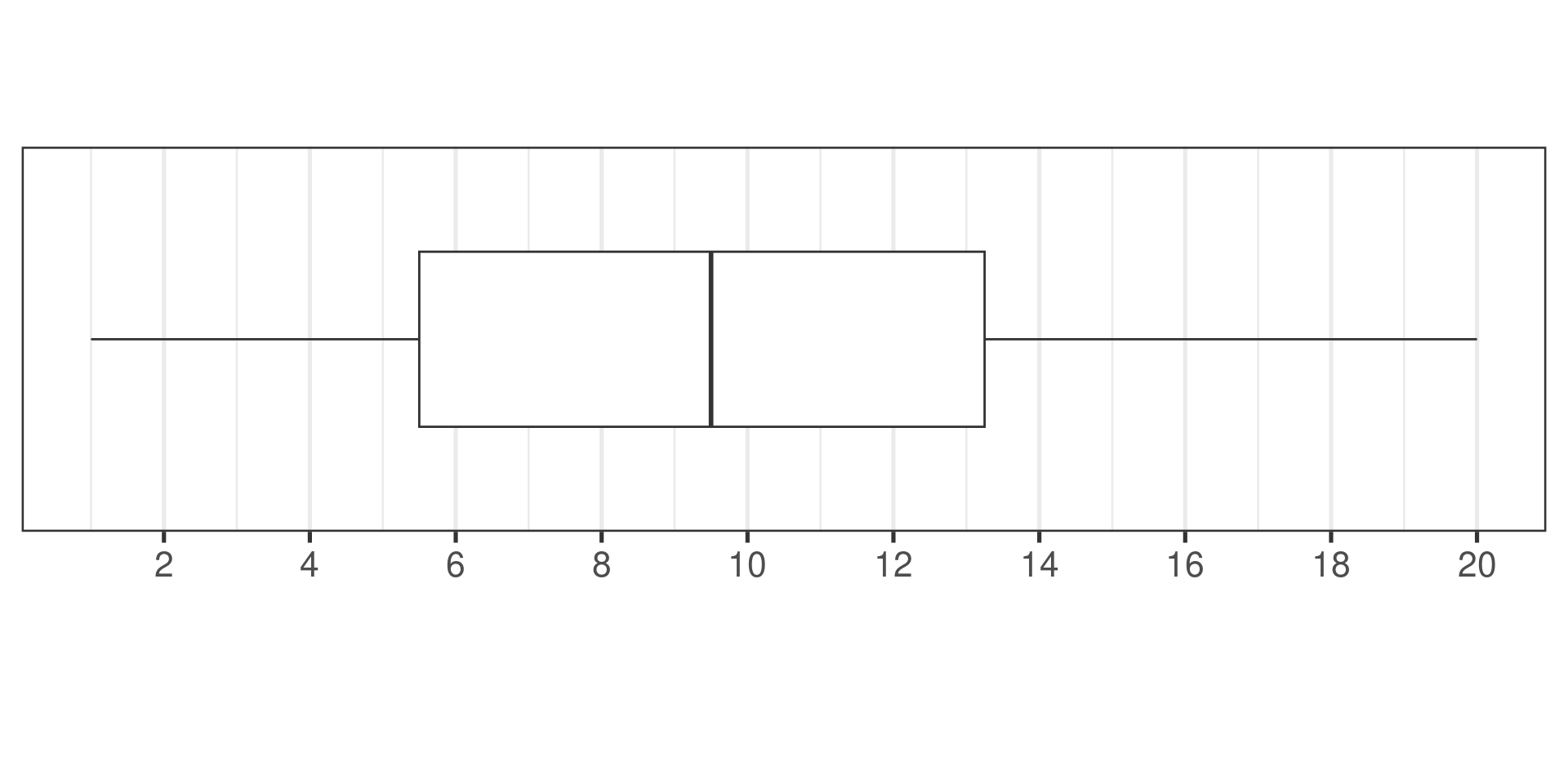
Five numbers summary:

  • Minimum

  • First quartile

  • Second quartile (median)

  • Third quartile

  • Maximum

Five numbers summary:

1 1 2 4 6 7 7 9 10 10 10 13 14 15 16 20
Min Q1 Median Q3 Max
1 5 9.5 13.5 20

Mean

1 1 2 4 6 7 7 9 10 10 10 13 14 15 16 20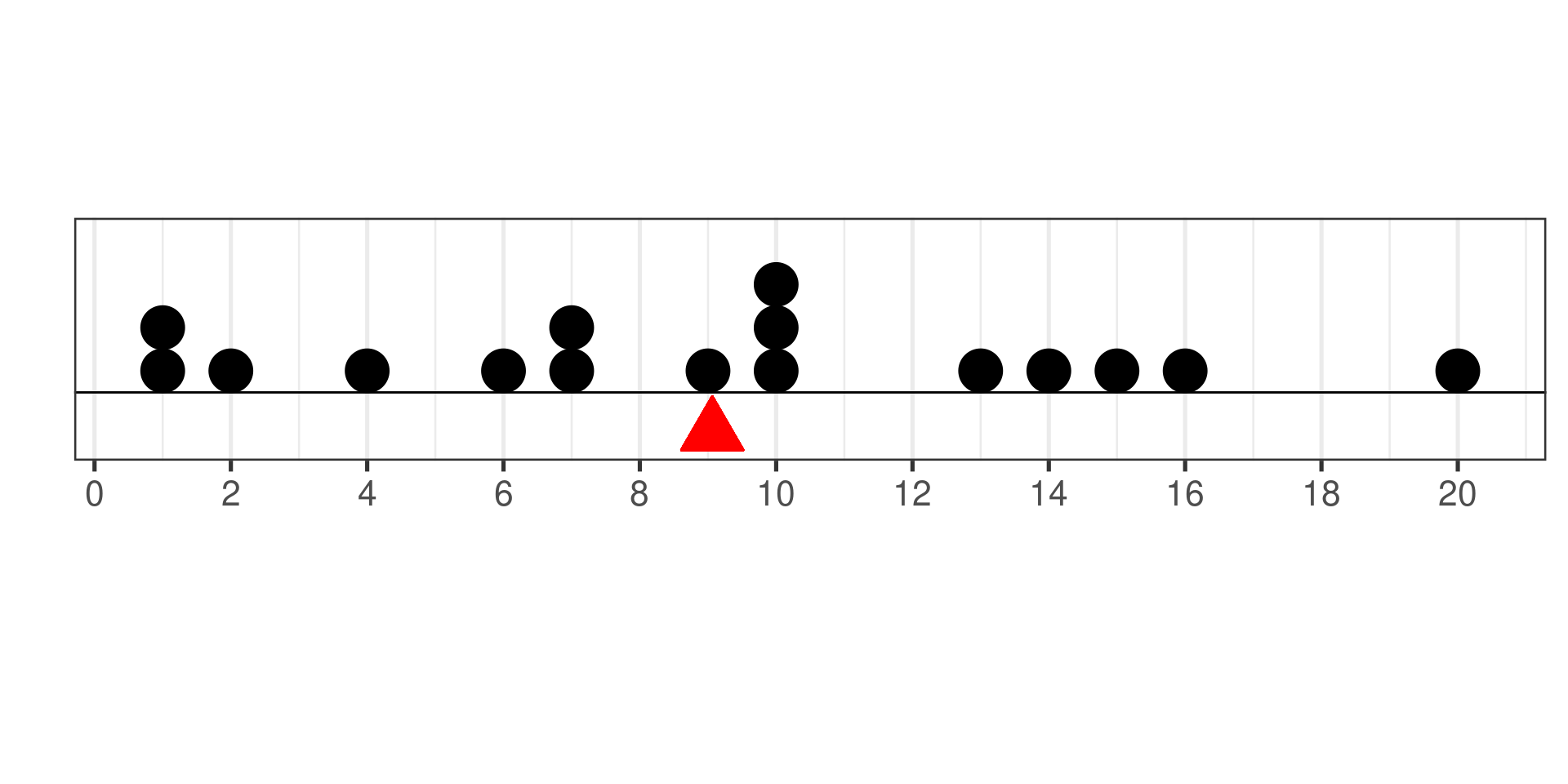

Standard Deviation

1 1 2 4 6 7 7 9 10 10 10 13 14 15 16 20

 

12345678910111213141516171819209.062513−9.06256−9.062520−9.06251−9.0625deviation:𝑥−𝑥=13−9.0625=3.9375deviation:𝑥−𝑥=6−9.0625=−3.0625deviation:𝑥−𝑥=20−9.0625=10.9375deviation:𝑥−𝑥=1−9.0625=−8.0625variance=”mean”ofsquaresofallthedeviationsvariance=1𝑛−1∑(𝑥−𝑥)2standarddeviation:𝑠=√variance

  • Mean: \(9.0625\)

  • Deviations: \(x - 9.0625\)

  • Square deviations: \((x - 9.0625)^2\)

  • Sum of square deviations: \[\sum (x - 9.0625)^2\]

  • Variance: \[\frac{1}{15}\sum (x - 9.0625)^2\]

  • Standard Deviation: \[\sqrt{\frac{1}{15}\sum (x - 9.0625)^2} = 5.5912879\]

Histogram