Math 132A
Binomial Distributions - mean and s.d.
Bernoulli Random Variables
Bernoulli Trial: an experiment with exactly two outcomes:
- success, with probability \(p\)
- failure, with probability \(1 - p\)
Bernoulli Random Variable: a random variable \(B\) with two possible values:
- 1, with probability \(p\)
- 0, with probability \(1 - p\)
\(B \sim \operatorname{Binom}(1, p)\)
Expected Value of Bernoulli Variable
| \(x\) | \(0\) | \(1\) |
|---|---|---|
| \(P(B = x)\) | \(1 - p\) | \(p\) |
Examples
Flipping a fair coin
Rolling a fair die
Variance of Bernoulli Variable
| \(x\) | \(0\) | \(1\) |
|---|---|---|
| \(P(B = x)\) | \(1 - p\) | \(p\) |
Binomial Random Variables
\(X \sim \operatorname{Binom}(n, p)\)
\(X\) is the sum of \(n\) independent Bernoulli random variables, each with the same probability of success \(p\).
\(X = B_1 + B_2 + B_3 + \cdots + B_n\)
Mean of a Binomial Random Variable
\(X = 1\cdot B_1 + 1\cdot B_2 + 1\cdot B_3 + \cdots + 1\cdot B_n\)
\(\displaystyle \begin{aligned} \operatorname{E}X &= 1\cdot {\color{red}\operatorname{E}(B_1)} + 1\cdot {\color{red}\operatorname{E}(B_2)} + 1\cdot {\color{red}\operatorname{E}(B_3)} + \cdots + 1\cdot {\color{red}\operatorname{E}(B_n)}\\[12pt] &\class{fragment}{{}= 1\cdot {\color{red}p} + 1\cdot {\color{red}p} + 1\cdot {\color{red}p} + \cdots + 1\cdot {\color{red}p}}\\[12pt] &\class{fragment}{{}= {\color{red}p} + {\color{red}p} + {\color{red}p} + \cdots + {\color{red}p}}\\[12pt] &\class{fragment}{{}= n\cdot {\color{red}p}} \end{aligned}\)
Variance of a Binomial Random Variable
\(X = 1\cdot B_1 + 1\cdot B_2 + 1\cdot B_3 + \cdots + 1\cdot B_n\)
\(\displaystyle \begin{aligned} \operatorname{Var}X &= 1^2\cdot {\color{red}\operatorname{Var}(B_1)} + 1^2\cdot {\color{red}\operatorname{Var}(B_2)} + 1^2\cdot {\color{red}\operatorname{Var}(B_3)} + \cdots + 1^2\cdot {\color{red}\operatorname{Var}(B_n)}\\[12pt] &\class{fragment}{{}= 1^2\cdot {\color{red}p(1-p)} + 1^2\cdot {\color{red}p(1-p)} + 1^2\cdot {\color{red}p(1-p)} + \cdots + 1^2\cdot {\color{red}p(1-p)}}\\[12pt] &\class{fragment}{{}= {\color{red}p(1-p)} + {\color{red}p(1-p)} + {\color{red}p(1-p)} + \cdots + {\color{red}p(1-p)}}\\[12pt] &\class{fragment}{{}= n\cdot {\color{red}p(1-p)}} \end{aligned}\)
Summary
Suppose \(X \sim \operatorname{Binom}(n, p)\). Then
- \(\operatorname{E}X = \mu_X = np\)
- \(\operatorname{Var} X = np(1-p)\)
- \(\operatorname{SD} X = \sigma_X = \sqrt{np(1-p)}\)
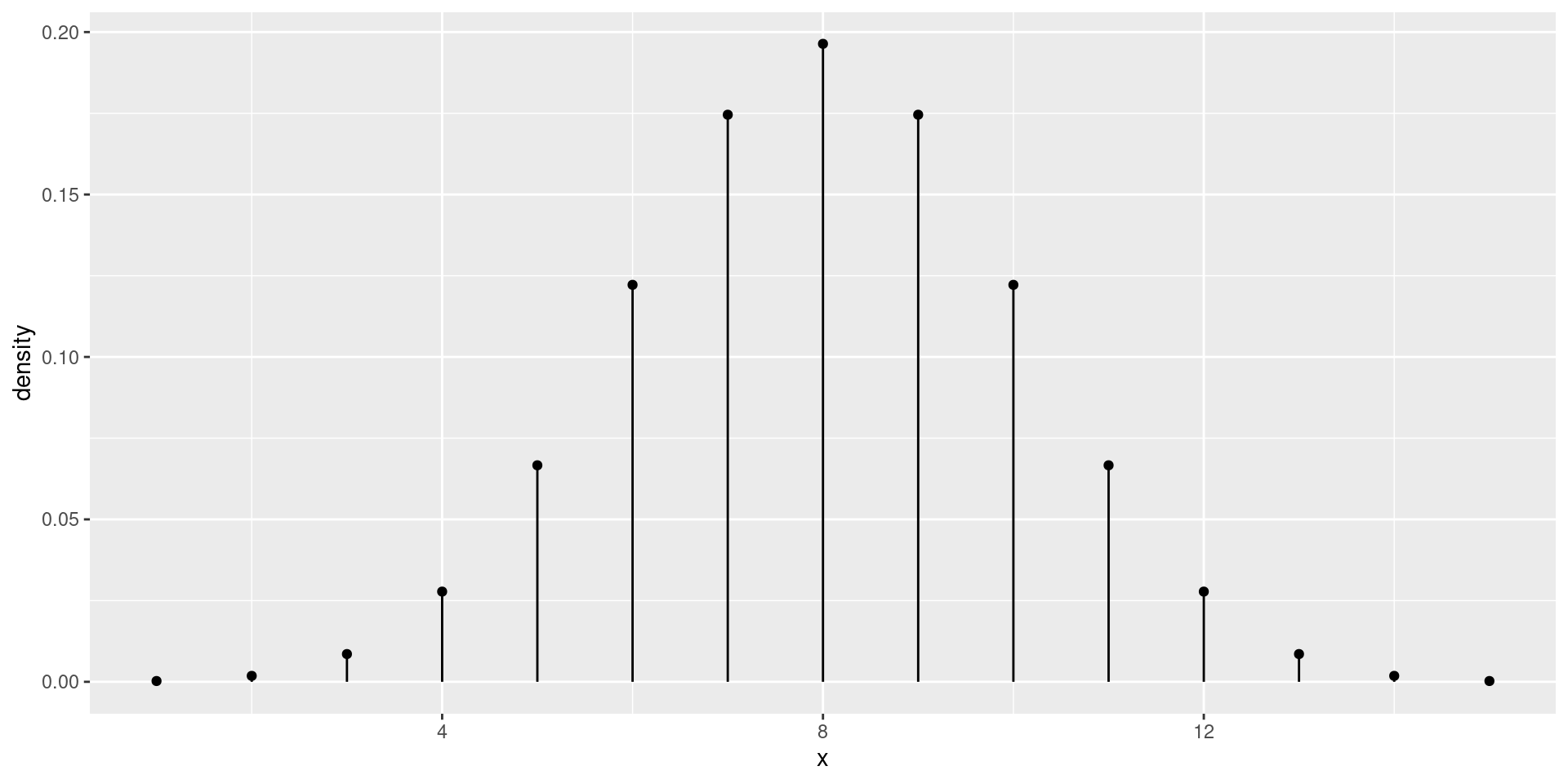
Example (16 fair coins)
\(X = {}\) the number of heads when we flip 16 fair coins.
\(X \sim \operatorname{Binom}(16, 1/2)\)
Distribution (16 fair coins)
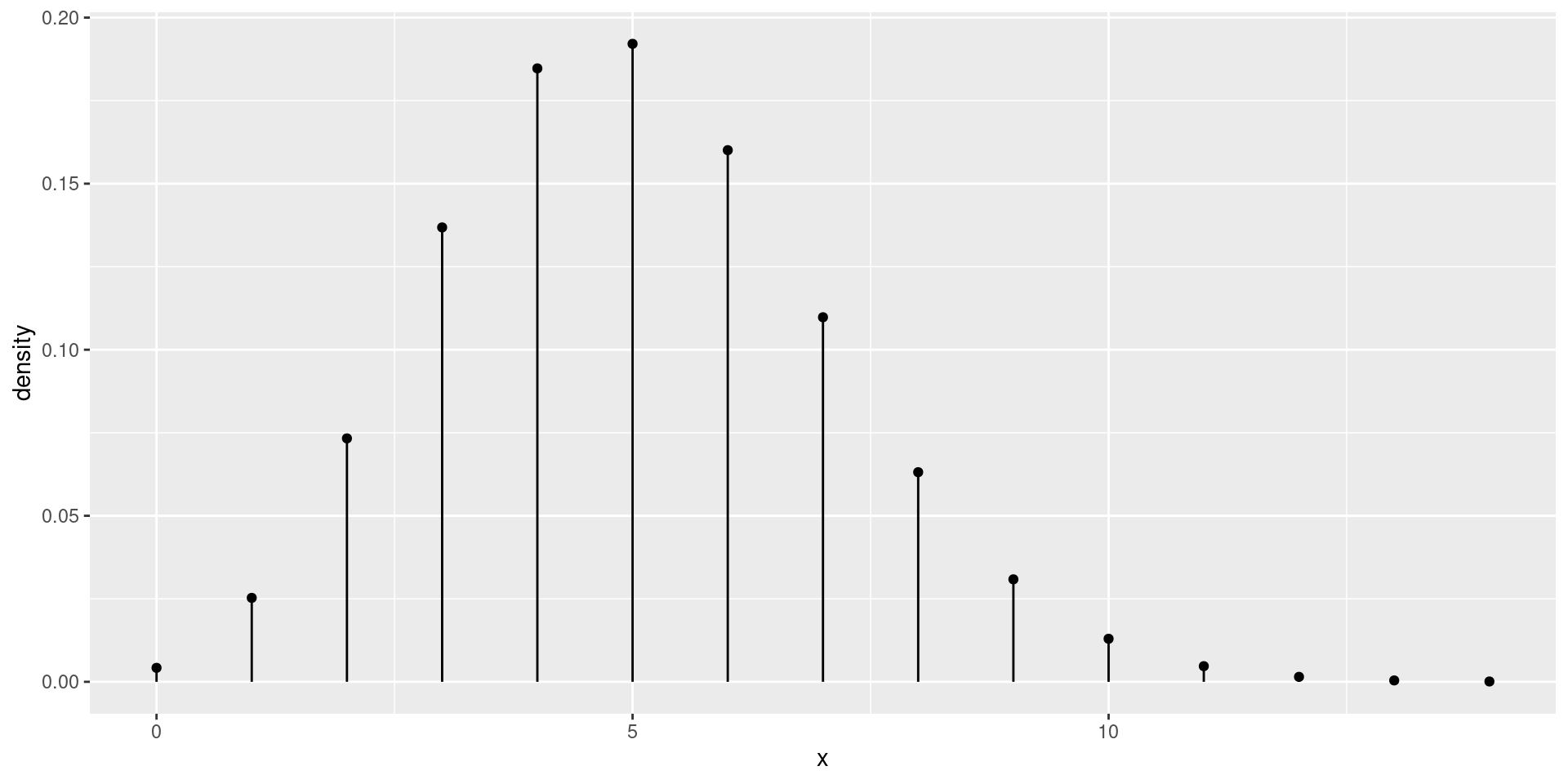
Example (10 fair dice)
\(X = {}\) the number of sixes when we roll 10 fair dice
\(X \sim \operatorname{Binom}(10, 1/6)\)
Distribution (10 fair dice)
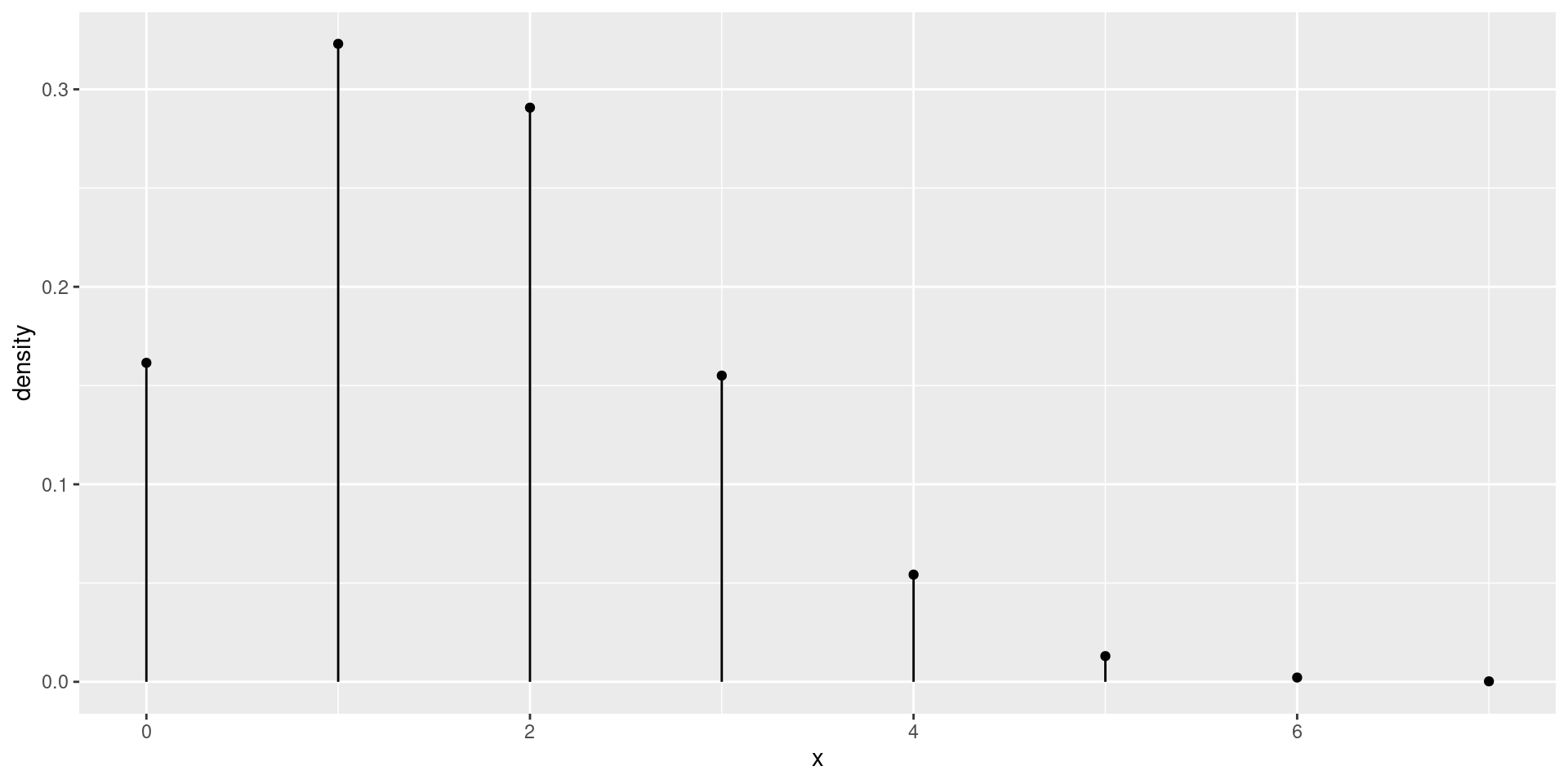
Example (30 fair dice)
\(X = {}\) the number of sixes when we roll 30 fair dice
\(X \sim \operatorname{Binom}(30, 1/6)\)
Distribution (10 fair dice)